THE IMPACT OF DSM V ON PSYCHIATRIC RESEARCH
Abstract
The publishing of DSM V represents a challenge, not only for the categorical systematization of psychiatry, but also for psychiatric research. The paper discusses the possible and predictable impact of the DSM V on research, in three domains: 1. Clinical and longitudinal studies, 2. Fundamental research, 3. The anthropologic dimension of psychiatry. The orientation of DSM V towards the s p e c t r u m p e r s p e c t i v e a n d d e v e l o p m e n t a l psychopathology, as well as the invitation for the assessment of all the synchronic and diachronic comorbidities, will potentially require the elaboration of new methodologies for research. The fundamental research will probably correlate the study of the main cerebral functions with an evolutionary approach. The anthropologic dimension of psychiatry tends to focus on narrativity, case studies, as well as on a clear definition of conceptual terms, such as “psychosis”.
The DSM V (1) is a clear and approachable manual, giving explicit answers for the majority of questions that could arise. It will surely have an important impact, not only on psychiatric practice, but also on research. The manual maintains the categorical structure, so that the studies based on DSM-IV-TR (2) can be used in the future. However, the important novelties of DSM V will probably induce a crisis in the psychiatric research, a crisis that will involve the necessity to re-evaluate the methodologies for research.
This paper reviews some of the possible problems that could arise concerning: 1. clinical research, 2. fundamental research and 3. anthropological research. But, firstly, we will mention some of the novelties introduced in the DSM V.
These novelties are mostly a consequence of the tension between the categorical and the dimensional approaches. The outcome is an approach based on developmental psychopathology and a spectrum perspective. Therefore, DSM V takes a few steps towards ICD 10: – the removal of the axis system; – the use of the WHODAS system (3) for the evaluation of social dysfunction; – the use of the Z codes from ICD 10 (4), which allows for the synchronic and diachronic contextualization of cases; – the acceptance of some specific nosological categories: for example, the Obsessive-Compulsive and Related Disorders, which form a distinctive class.
The aspects of the DSM V that suggest the developmental perspective are the order of the chapters and the recommendation to assess all long-life psychopathological experiences of the patient. As for the spectrum perspective, this is being expressed by grouping similar disorders in distinct classes, which, in some cases, explicitly take the name of spectrum: the Autism Spectrum Disorders, the Schizophrenia Spectrum Disorders etc. In a similar manner, Bipolar Disorders, Depressive Disorders, Anxiety Disorders, Obsessive- Compulsive Disorder etc. are organized. The spectrum concept has imposed itself in the past 20 years, so it seems natural to be used in DSM V (5,6,7,8). However, this is a diagnostic manual and it cannot integrate the whole concept of spectrum, because parts of it expand towards normality: subclinical manifestations, temperamental traits, bio-psychic markers, professional preferences etc. Moreover, these aspects can also be present in the first- degree relatives of patients.
1. THE PROBLEM OF COMORBIDITIES, CLINICAL FIELD-TRIALS AND NATURALISTIC STUDIES
DSM V encourages the assessment of all the synchronic and diachronic comorbidities of the patient. This can have an important impact on the clinical Field- Trials, because it will be difficult to find “pure cases”, specific to a category, when considering the life history. Therefore, new research methodologies will be necessary, at least in the area of psychotropic medication research. One solution could be to undertake studies in two phases:
in a first phase – to include the whole class of a spectrum (e.g. autism, bipolar, anxiety, schizophrenia, OCD spectrum etc.) and in a second phase – to focus on a specific diagnostic category or subgroup and find its distinctive aspects.
Other methodological problems, in more specific domains, will probably occur. The issue of comorbidity is significant. For example, depression is not only a clinical category or disorder. It is frequently comorbid with almost all the categorical disorders. There are cases in which it is officially included in the diagnosis, as in the case of schizophrenia. In other cases, it is a common comorbidity, for example in OCD or persistent delusional disorders. Hence, the studies can divide these disorders in two subgroups: with or without depression.
The problem of the “overlap of spectra” must be mentioned as well. A. Marneros and H. Akiskal discuss it in their book:”The Overlap of Affective and Schizophrenic Spectra” (9). From this perspective, schizoaffective episodes and schizoaffective disorder can be considered a “meeting point” between schizophrenia and mood disorders (10,11). The depressive and manic episodes with psychotic features can be interpreted as an overlap of mood disorders and persistent delusional disorders. These issues lead to some theoretical problems concerning the meaning of different concepts: psychosis, delusion, schizophrenia, unitary psychosis. Examples from non-psychotic areas can be: the overlap of the anxiety class (spectrum) and bipolar class (spectrum), represented by cyclothymia; the case of agoraphobia, which worsens during depressive periods and improves spontaneously during hypomanic ones, could express an overlap of anxiety and the bipolar spectrum.
Other difficulties for clinical research refer to mixed or transitional episodes of two categories (or disorders), such as anxious-depressive or mixed manic- depressive states. The transition between the symptoms in OCD and involuntary movements or impulsive behaviours, suggested by Hollander (12), should also be kept in mind.
As a conclusion to this part, we can say that the orientation of DSM V towards the spectrum and developmental perspectives will require the elaboration of new research strategies.
2. FUNDAMENTAL RESEARCH IN PSYCHIATRY: T H E N E U R O B I O L O G I C A L A N D EVOLUTIONARY PERSPECTIVES
Theoretically, the DSM III (13) encouraged cognitive-behavioural research, based on studies of the brain – and neuroscience in general – as fundamentals for understanding psychopathology. This orientation is integrated in the stress/vulnerability doctrine, which includes genetic and neuro-developmental factors, leading to important scientific progress in the domain. Besides the intensive study of neurotransmitters, another approach contributed to this progress: the emergence and development of evolutionary psychopathology, oriented towards the study of “psychic modules”.
Some remarkable scientific discoveries in psychiatry were the identification of the neurocognitive dysfunctions in schizophrenia and the framing of the concept of “social cognition”. Social cognition was intensively studied in the field of autism. It has been proven that one of the functions of the “social brain”, called “Theory of Mind” (ToM) (the ability of guessing someone else’s intentions in a certain situation), is not adequately developed by the age of 3 in autism (14). The “social brain” is considered to be a phylogenetically inherited gain during anthropogenesis, useful for the collaboration between people living in small groups (15). Other domains of social cognition are the emotion recognition and the attributional style. Research of social cognition was correlated with the study of attachment theory, both of them leading to a better understanding of psychopathological conditions, such as phobic anxiety, paranoid delusions or personality disorders.
However, ToM deficits could not explain all of the semiological phenomena of autism. The impairment of another global function, called by Uta Frith “the central coherence” (16, 17), was related to important symptoms, such as: the intolerance for change, the importance given to details, the deficiency in perceiving the whole etc. Central coherence refers to the ability of processing and integrating details and information in an ensemble, detaching itself from the context. This function is also impaired in schizophrenia and obsessive-compulsive disorder, a condition in which there is an excessive preoccupation for order, details, repetition, hoarding etc. In OCD, a third neuro-psychological global function is impaired: the “executive functions” (18), referring to the planning and control of performing a purposeful action. In autism, there is a deficit of all the three functions – ToM, central coherence, executive functions – as well as of verbal and non-verbal communication. Autism became a disorder of reference in the study of fundamental neuropsychological functions in humans. However, deficits of these functions exist in other psychiatric disorders as well.
The experimental studies, which identified the deficiency of ToM in autism, were correlated by Baron- Cohen with the evolutionary doctrine (19). Crow’s evolutionary approach (20) also suggests that psychosis (especially schizophrenia) is a price paid by the evolution of human brain for the development of articulated language 150000 years ago, a process connected to the interhemispheric asimmetry. Burns’ theory (21) is similar, considering that psychosis (schizophrenia) is a consequence of the development of the social brain, during the same period of time. The evolutionary approach and neurocognitive research are not disconnected. Both central coherence and executive functions are correlated with the neurocognitive dysfunctions identified in schizophrenia, the disorder Crow and Burns referred to. Moreover, the evolutionists agree that another important gain during anthropogenesis is the self-control of the aggressive impulses towards other persons (22). Self-control is impaired in more areas of OCD: in aggressive obsessions, in the egodystonic hypercontrol of the obsessions related to taboos, in the control of all deliberate actions. (23) (The obsessive verification is considered an impairment of the adaptive self-control of behaviour.)
T h e e v o l u t i o n a r y d o c t r i n e i n t e r p r e t s psychopathological conditions to represent deficits of adaptive psychological mechanisms (24), from the perspective of Fodor’s “psychic modules” (25). This view was analyzed in the field of depression, anxiety, agoraphobia, ADHD, manic states etc., giving way to two questions: What are the neuropsychological foundations of these “adaptive psychic modules”, which are evolutionarily selected and genetically transmitted? and What are the dysfunctional cerebral mechanisms which transform these modules – for example depression, control of behaviour etc. – from adaptive to non-adaptive ones?
The problems raised by evolutionary psychiatry are partly theoretical, attempting to answer the question: What is mental disorder? (26) But the correlation with the fundamental psychiatric research remains significant if we consider the consequences of research in autism. That is probably why the National Institute of Mental Health in the USA (NIMH), during the elaboration of DSM V, turned to the strategy of fundamental research in psychiatry, leading to the development of the Research Domain Criteria Project (RDoC) (27,28). The assumption of the project was that psychopathological syndromes are based on dysregulations of neurobiological systems and brain circuits and that these dysfunctions could be identified with the instruments of neuroscience (electrophysiology, functional neuroimaging etc.). 5 major research domains were identified, with each one including more specific areas:
– N e g a t i v e Va l e n c e S y s t e m s ( F e a r / E x t i n c t i o n , Stress/Distress, Agression)
– P o s i t i v e Va l e n c e S y s t e m s ( R e w a r d s e e k i n g , Reward/Habit learning)
-Cognitive Systems (Attention, Perception, Working Memory, Language behaviour, Cognitive/effortful control)
-Systems for Social Processes (Imitation, theory of mind, Social dominance, Facial expression identification, Attachment/Separation fear, Self-representation )
-Arousal/Modulatory Systems (Arousal and regulation, Resting state activity)
Each of these domains can be studied by using seven classes of variables: genes, molecules, cells, neural circuits, physiology, behaviours and self-reports.
The fundamental research in psychiatry, organized and financed by the NIMH, is, apparently, not related to the clinical categories and their systematization in classes or spectra. Still, the connection between them exists. This is because, although fundamental studies are based on a psychobiological perspective, researchers will have to find psychiatric cases that are as pure as possible. The issues that have been mentioned in the first part of the article are also important for the RDoC project.
3. DSM V AND THE ANTHROPOLOGICAL VIEW IN PSYCHIATRIC RESEARCH
The anthropological perspective cannot be ignored in psychiatric research. Since 100 years ago, when Jaspers’ “General Psychopathology” (29) was published, it could not be contested that more than 70% of the psychiatric semiology includes subjective experiences, only partially communicated spontaneously or expressed verbally (30). This aspect led to the elaboration of structured and semi-structured interviews, such as the SCAN-WHO (31). Moreover, during the last two decades, the neophenomenological psychopathology has developed, being correlated with cognitivism (32).
Together with the philosophy of mind (33), it highlights the subjective “first person” perspective, different form the objective “third person” one (34).
Another anthropological aspect of psychiatry is the fact that it is based, more than other medical branches, on narrativity (35,36). Human beings are able to transpose memories, episodic or biographic ones, in stories with dramatic scenarios and heroes. In these stories, the subject is constantly the hero of reference. The narrative instance is the background for the emergence of “human cases”, as well as of “psychiatric cases”. Psychopathology first
developed in the 19th century, as a description of certain syndromes, based on the “faculties psychology” (cognition, volition, affectivity). In the 20th century, after Jaspers, psychopathology was personalized and became focused on the concept of the “conscious I” (Ich Bewusstsein). As a consequence, psychiatry started to give attention to the “ideal case” (37,38). This “ideal case” could “enlighten” a clinical issue, more than a statistical sum of some impersonal items would be able to. The “case of reference” – similarly to the cases used by legal advisers
– was then doubled by the “robot cases” (a synthesis of cases which are specific to a category). The operational definitions introduced by the DSM III-IV make this “robot case” more flexible, offering the possibility of various subtypes. Still, the case studies were not abandoned, having accompanied the DSM III-IV manuals and playing a very important role for the elaboration of the ICD 10 (39).
In the spirit of this tradition, around DSM V, various authors are promoting the prototypical diagnosis (40), by taking the elements of “robot cases”. Because the DSM IV TR was criticized for its hypo-narrativity (41), DSM V now encourages narrativity. Actually, the official inclusion of the Z codes from ICD 10 in the DSM V allows and even invites clinicians to a synchronic and diachronic contextualization of cases. “Relational disorders” (42) can be analyzed in this manner. The efforts of the former president of the WPA, Juan Mezzich, concerning the “person-centred diagnosis” in psychiatry (43) are therefore included, in the approach of DSM V.
The use of conceptual terms is another important aspect of psychiatric anthropological research. DSM III abandoned the concept of “neurosis” and changed the significance of the notion of “endogenous psychosis”. The expression “psychosis” is used in the DSM III-IV only as an ostensive definition, which refers to syndromes such as delusions, non-criticized hallucinations or verbal disorganization. In the period preceding the publishing of DSM V, the interest for psychosis has grown, leading to the formation of a working group, in order to discuss the approach of psychosis in the DSM V. Unlike the DSM III- IV, where mania and inhibited depression were not included among psychoses, the researchers who have been active in this particular field are accepting 5 dimensions of psychosis (44).
Currently, the great majority of today’s researchers and theoreticians accept a “psychotic spectrum” (45) that includes agitated mania and inhibited depression. This doctrine includes Crow’s evolutionary perspective, the research project of “early psychosis” (46), as well as other monographies and research studies (47). DSM V is reticent to this view, which gives psychosis a larger meaning.
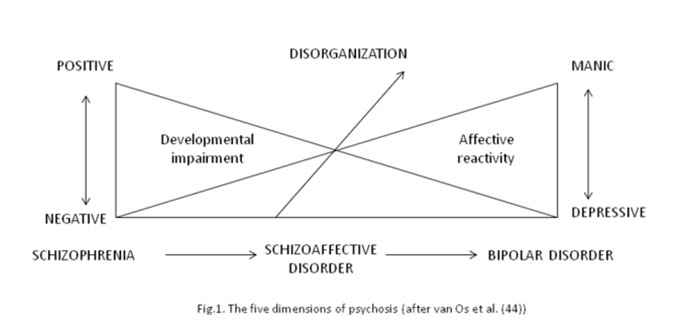
That is the reason why the DSM V would rather wait and see, taking the definition of psychosis out from the Glossary of technical terms.
An important concept for the psychopathology of the 20th century was the one of “consciousness”, based on the understanding of the “conscious I” (Ich Bewusstsein) in Jaspers’s view. The concept has faded in the modern age. Its place has been taken, in the last decades, by the concept of the “self” (48). Hence, in psychopathology, systematic researches were developed, based on neuroscience, which interpret schizophrenia as the dysfunction of different parts of the self (49). From this perspective, DSM V takes a step back from the DSM IV, by non-differentiating the diagnosis of schizophrenia. According to DSM V, any delusion with hallucinations can be diagnosed as schizophrenia and the bizarre character of the delusion is not necessary. This situation was somehow anticipated by European researchers (50), who conceptualize schizophrenia closer to the one in Bleuler’s view. They state that the hallucinatory delusion is a secondary phenomenon, different from the one encountered in Persistent Delusional Disorder.
DSM V accepts the concept of Self, but at a peripheral level, in the new elaboration of Personality Disorders, in section III. This chapter, which is very interesting and uses anthropological concepts, such as self-transcendence, empathy, intimacy etc., focuses on the concept of Self. But it will probably remain peripheral, because the absence of the axes does not force the users to assess the personality structure any more. This theme will probably concern a small group of specialists. Therefore, DSM V misses the direct connection with the synthetic research of anthropology, which would have been possible through a wider use of the concept of “Self”. The manual stays focused on a biopsychomedical approach. This aspect is obviously correlated with the research project of NIMH that we have already mentioned.
This does not mean that the anthropological psychiatric research will not continue. Naturally, it will develop and influence, by means of feedback, the development of the DSM VI.
In conclusion, the publishing of DSM V constitutes a challenge for future psychiatric research, both for clinical and fundamental research, as well as and for the anthropological dimension of psychiatry. The research of years to come will attempt a response to this challenge.
The DSM V stresses that clinicians should b e c o m e m o r e r e s p o n s i b l e r e g a r d i n g d i a g n o s i s formulation. In science, the manual invites to proceed to a synthetic approach, which would attempt to reunite clinical research, experimental studies, alongside the doctrinary orientation. This issue is currently supported by an ongoing trend supporting the extensive concept of the Self. (51).
REFERENCES
1.American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 5th edn. Washington, D.C.: American Psychiatric Publishing, 2013.
2.American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 4th edn, Text Revision. Washington, D.C.: American Psychiatric Association, 2000.
3.World Health Organization. Measuring health and disability: manual for WHO Disability Assessment Schedule (WHODAS 2.0). Geneva: World Health Organization, 2010.
4.World Health Organisation. Multiaxial Presentation of the ICD-10 for use in Adult Psychiatry. Cambridge University Press, 1997.
5.Akiskal HS, Pinto O. The soft bipolar spectrum: footnotes to Kraepelin on the interface of hipomania, temperament and depression. In: Marneros A, Angst J (eds). Bipolar disorders: 100 years after manic depressive insanity. Dordrecht: Kluwer, 2002, 37–62.
6.Amarel DG, Dawson G, Geschwind DH (eds). Autism Spectrum Disorders. New York: Oxford University Press, 2012.
7.Frank E, Rucci P, Cassano GB. One way forward for psychiatric nomenclature: The example of the Spectrum Project approach. In: Regier DE, Narrow WE (eds.). The Conceptual Evolution of DSM-5. Washington D.C., London, England: American Psychiatric Publishing, 2011.
8.Ritsner MS. Handbook of Schizophrenia Spectrum Disorders. Berlin, Heidelberg: Springer, 2011.
9.Marneros A, Akiskal H (eds.). The Overlap of Affective and Schizophrenia Spectrum. Cambridge University Press, 2007.
10.Marneros A, Pillman F (eds.). Acute and Transient Psychoses. Cambridge University Press, 2004.
11.Marneros A, Tsuang MT (eds.). Affective and Schizoaffective Disorders. Berlin, Heidelberg: Springer, 1990.
12.Hollander E, Wong CM (eds.). Obsessive-compulsive related disorders. Washington, D.C.: American Psychiatric Press, 1993.
13.American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 3rd edn. Washington, DC: American Psychiatric Press, 1980.
14.Baron-Cohen S, Targer-Flusberg H, Cohen D (eds.). Understanding other minds: perspectives for autism. New York: Oxford University Press, 2005.
15.Dunbar RIM, Barrett L (eds.). The Oxford Handbook of Evolutionary
Psychology. New York: Oxford University Press, 2007.
16.Frith U, Happe F (eds.). Autism beyond theory of mind. Cognition 1994; 50: 115-132.
17.Happe F. Central coherence and theory of mind in autism: reading hemographs in context. British Journal of Developmental Psychology 1997; 15:1-12.
18.Baron-Cohen S, Swettenham J. Theory of mind in autism: its relationship to executive function and central coherence. In: Cohen D, Volkmar F (eds.). Handbook of Autism and Pervasive Developmental Disorders, 2nd Edition. John Wiley and Sons, 1997.
19.Baron-Cohen S. Mindblindness: An Essay on Autism and Theory of Mind. London: MIT Press, 1997.
20.Crow TJ. A Darwinian approach to the origins of Psychosis, BJP 1995; 167:12-25.
21.Burns JK. The Descent of Madness. Evolutionary Origins of Psychosis and the Social Brain. London: Routledge, 2007.
22.Brüne M. Textbook of Evolutionary Psychiatry: The Origins of Psychopathology. New York: Oxford University Press, 2008.
23.Lăzărescu M, Bumbea O. Patologie obsesivă. Bucuresti: Editura Academiei Române, 2008.
24.Wakefield JC. Evolutionary versus prototype analyses of the concept of disorder. Journal of Abnormal Psychology 1999;1008: 374-399.
25.Fodor JA. Modularity of Mind: An Essay on Faculty Psychology. Cambridge, Mass: MIT Press, 1983.
26.Bolton D. What is mental disorder? An essay in philosophy, science, and value. Oxford University Press, 2008.
27.First M. Beyond clinical utility: broadening the DSM-V research appendix to include alternative diagnostic constructs. American Journal of Psychiatry 1006;163: 1679-81.
28.Insel T, Cuthbert B, Garvey M et al. Research Domain Criteria (RDoC): Toward a New Classification Framework for Research on Mental Disorders. Am J Psychiatry 2010;167(7): 748-51.
29.Jaspers K. General Psychopathology. Baltimore and London: Johns Hopkins University Press, 1997.
30.Oyebode F. Sims’ Symptoms in the Mind. An Introduction to Descriptive Psychopathology. Elsevier, 2008.
31.World Health Organization. Schedules for Clinical Assessment in Neuropsychiatry (SCAN). Geneva: WHO, 1992.
32.Gallagher S, Schmicking D (eds.). Handbook of Phenomenology and cognitive Science. Springer, 2010.
33.McLaughlin BP, Beckermann A, Walter S (eds.). The Oxford Handbook of Philosophy of Mind. Oxford University Press, 2009.
34.Zahavi D. Subjectivity and selfhood: investigating the first person perspective. Cambridge, MA: MIT Press, 2005.
35.McAdams DP. Personal Narratives and the Life Story. In: John OP, Robins RW, Pervin LA (eds.). Handbook of Personality. Theory and Research. New York, London: Guilford Press, 2008, 242-264.
36.Harre’ R. The logical basis of psychiatric meta-narratives. In: Chung MC, Fulford KWM, Graham G. (eds.). Reconceiving Schizoprenia. Oxford: Oxford University Press, 2007, 295-305.
37.Wiggins OP, Schwartz MA. Research into Personality Disorders: the Alternatives of Dimensions and Ideal Types. Journal of Personality Disorders 1991;5(1): 69-81.
38.Kraus A. Methodological problems with the Classification of Personality Disorders: the Significance of Existential Types. Journal of Personality Disorders 1991;5(1): 82-92.
39.Spitzer R. DSM-IV Casebook: A Learning Companion to the Diagnostic and Statistical Manual of Mental Disorders. American Psychiatric Association, 1994.
40.Ortigo KM, Bradley B, Westen D. An empirically based prototype diagnostic system for DSM-V and ICD-11. In: Millon T, Krueger R, Simonsen E (eds.). Contemporary directions in psychopathology: scientific foundations of the DSM-V and ICD-11. New York: The Guilford Press, 2010, 374–390.
41.Sadler JZ. Values and psychiatric diagnosis. Oxford: Oxford University Press, 2004.
42.Beach SRH, Wamboldt MZ, M.D, Kaslow NJ et al. Relational Processes and DSM-V: Neuroscience, Assessment, Prevention, and Treatment. Washington D.C., London, England: American Psychiatric Publishing, 2006.
43.Mezzich JE, Bergan CE, von Cranach M et al (eds.). Essentials of the
WPA International Guidelines for Diagnostic Assessment (IGDA). BJP 2003;182: s37-s39.
44.Tamminga CA, Sirovatka PJ, Darrel AR, van Os J (eds.). Deconstructing Psychosis: Refining the Research Agenda for DSM-V. Washington, D.C.: American Psychiatric Publishing, Inc, 2010.
45.Fujii D, Ahmed I (eds.). The Spectrum of Psychotic Disorders
Neurobiology, Etiology and Pathogenesis. Cambridge University Press, 2007.
46.McGorry, PD, Copolov DL, Singh BS. The Royal Park multi- diagnostic instrument for psychosis: part I: rationale & review. Schizophrenia Bulletin, 1990;16: 501-515.
47.Kingston T, Owoeye O, Kinsella A et al. Schizophrenic Spectrum Disorders in Relation to the Totality of Psychosis: From First Episode to Long-Term Outcome. In: Ritsner MS (eds.). Handbook of Schizophrenia Spectrum Disorders, vol. II. Springer, 2011, 269-279.
48.Gallagher S (eds.). The Oxford Textbook of the Self. Oxford University Press, 2011.
49.Kircher T, David A (eds.). The Self in Neuroscience and Psychiatry. Cambridge University Press, 2003.
50.Parnas JSS. DSM-IV and the founding prototype of schizophrenia: Are we regressing to a pre-Kraepelinian nosology? In: Kindler K, Parnas J. Philosophical Issues in Psychiatry II: Nosology. Oxford University Press, 2012, 237-259.
51.Lazarescu M. Bazele Psihopatologiei Clinice. Bucuresti: Editura Academiei Romane, 2010.
***



